Contents
Substitution and transposition are two basic techniques used in cryptography to transform plaintext into ciphertext.
Substitution ciphers involve replacing each letter or group of letters in the plaintext with another letter or group of letters according to a predetermined rule. The Caesar cipher is an example of a substitution cipher that shifts each letter of the message by a fixed number of places to the right or left of the alphabet. For example, if the shift is 3, the letter A would be replaced by D, B would become E, and so on. There are other types of substitution ciphers as well, such as the Atbash cipher, which replaces each letter with its reverse in the alphabet.
Transposition ciphers, on the other hand, involve rearranging the order of the letters in the plaintext to produce the ciphertext. The simplest form of transposition cipher is the columnar transposition cipher, which writes the plaintext in rows and then reads it out in columns. The order of the columns is determined by a keyword, which determines the order in which the columns are read. Other examples of transposition ciphers include rail fence and route ciphers.
Both substitution and transposition ciphers have weaknesses that can be exploited to decrypt a message. Substitution ciphers are vulnerable to frequency analysis attacks, where an attacker analyzes the frequency of letters or groups of letters in the ciphertext to deduce the key or plaintext. Transposition ciphers are vulnerable to known plaintext attacks, where an attacker uses knowledge of the plaintext to deduce the key or ciphertext. The security of an encryption algorithm is evaluated by its ability to withstand attacks that attempt to recover the original message.
Symmetric encryption
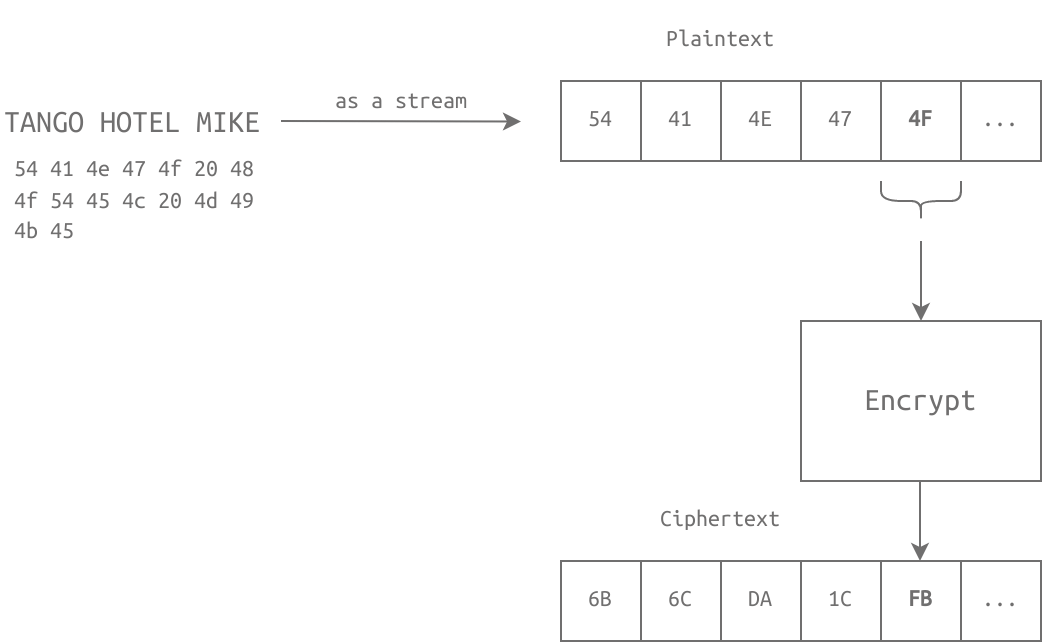
Symmetric encryption is a type of encryption where the same key is used for both encryption and decryption of data. This means that the sender and receiver of the data must have access to the same secret key in order to successfully encrypt and decrypt the message.
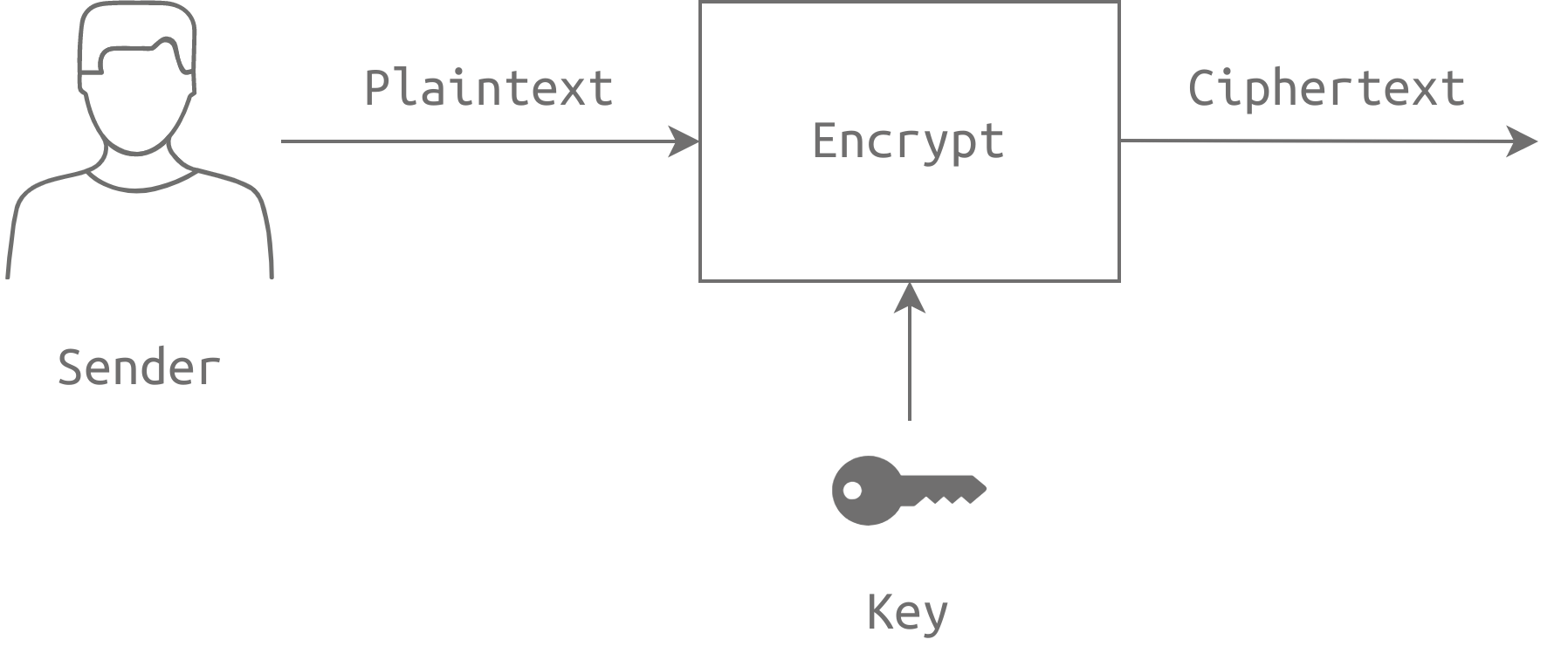
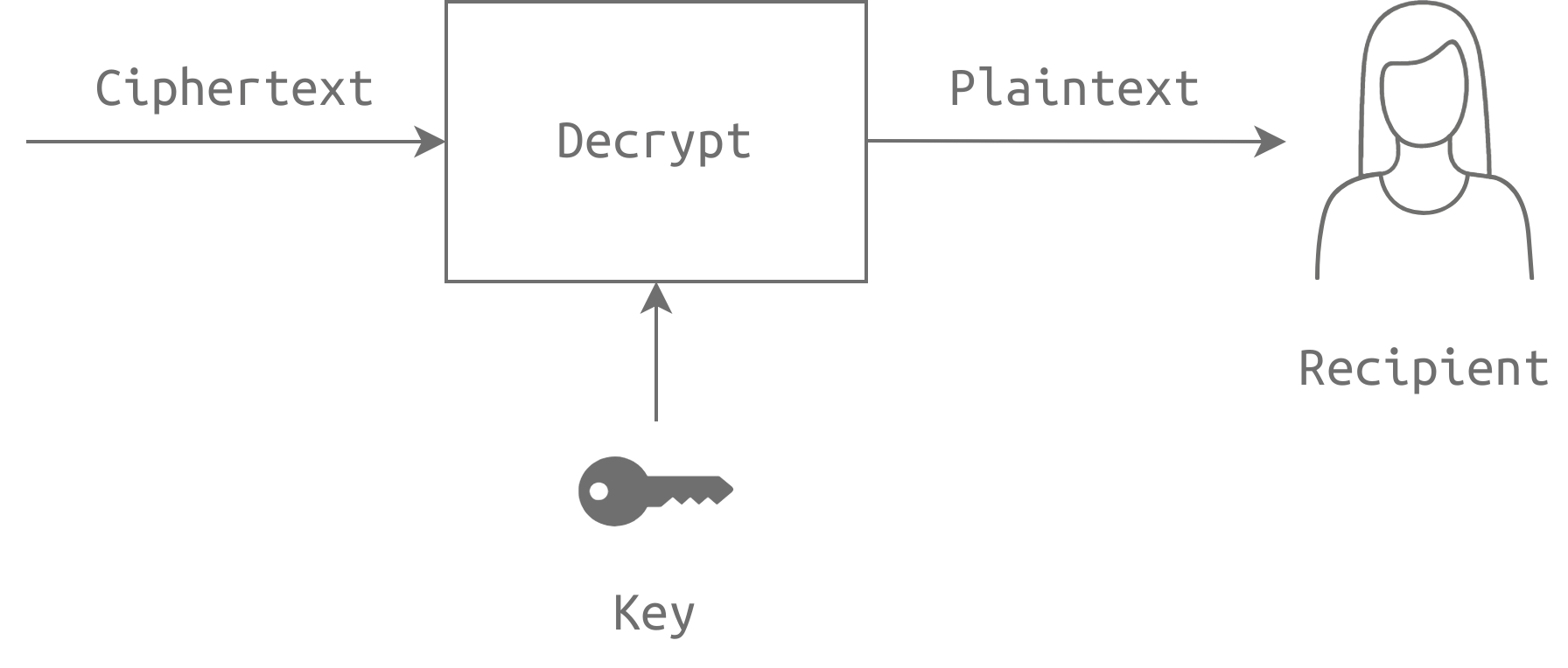
The cryptographic algorithm used for symmetric encryption takes the plaintext message and the secret key as input, and produces a ciphertext message as output. The plaintext message is the original message that needs to be protected, while the ciphertext message is the encrypted version of the plaintext message. The secret key is used to control the encryption process and ensure that the encrypted message cannot be easily decrypted without the key.
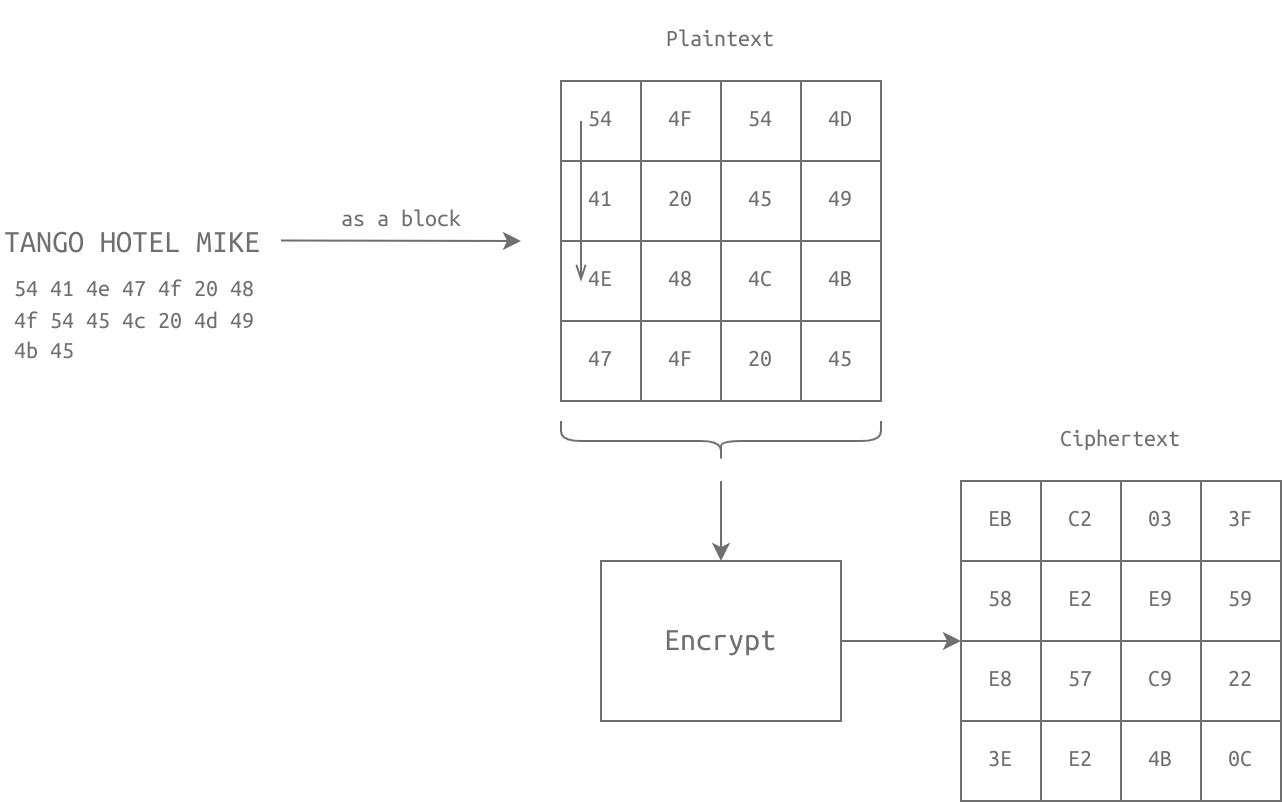
SubBytes(state): This transformation looks up each byte in a given substitution table (S-box) and substitutes it with the respective value. The state is 16 bytes, i.e., 128 bits, saved in a 4 by 4 array.
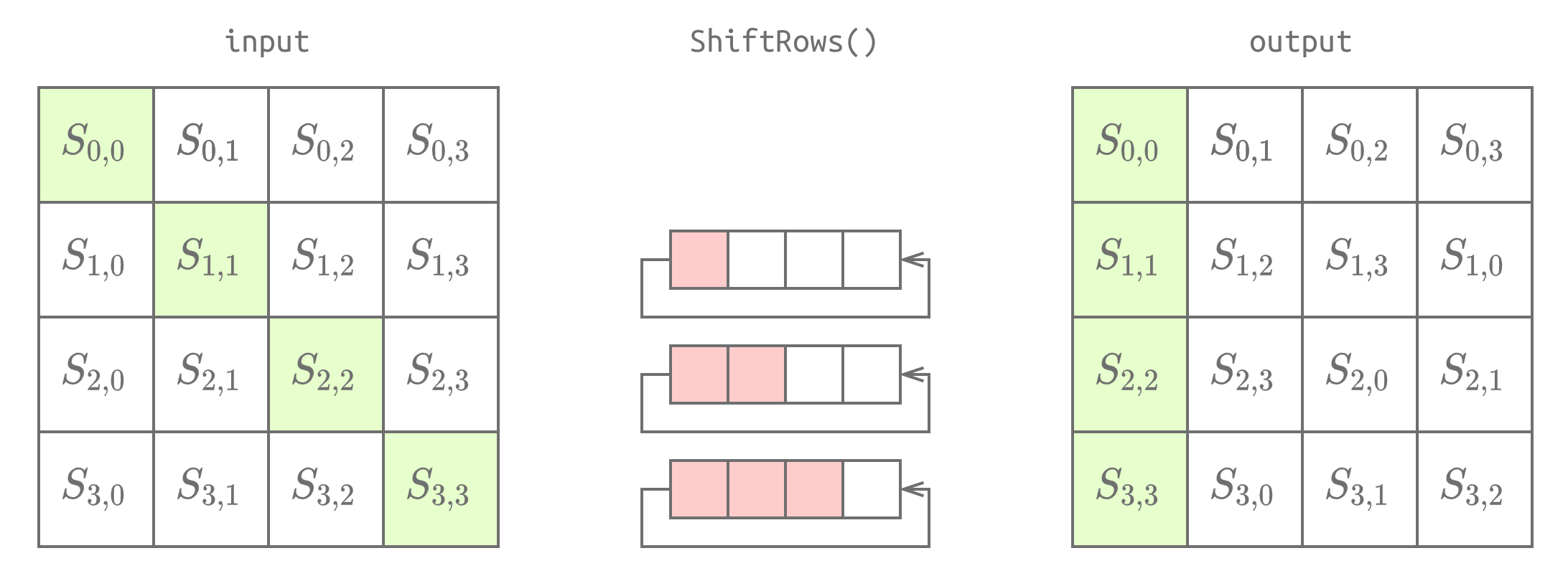
ShiftRows(state): The second row is shifted by one place, the third row is shifted by two places, and the fourth row is shifted by three places. This is shown in the figure below.
MixColumns(state): Each column is multiplied by a fixed matrix (4 by 4 array).
AddRoundKey(state): A round key is added to the state using the XOR operation.
Modern symmetric encryption algorithms like Advanced Encryption Standard (AES) are much more secure than ancient encryption algorithms like Caesar Cipher, because they use more complex mathematical operations and larger key sizes. AES is a block cipher algorithm, meaning that it encrypts data in fixed-size blocks, while stream ciphers encrypt data one bit at a time. AES supports key sizes of 128, 192, or 256 bits, and is widely used in many applications, including wireless networks, banking, and government communications.
| Encryption Algorithm | Notes |
|---|---|
| AES, AES192, and AES256 | AES with a key size of 128, 192, and 256 bits |
| IDEA | International Data Encryption Algorithm (IDEA) |
| 3DES | Triple DES (Data Encryption Standard) and is based on DES. We should note that 3DES will be deprecated in 2023 and disallowed in 2024. |
| CAST5 | Also known as CAST-128. Some sources state that CASE stands for the names of its authors: Carlisle Adams and Stafford Tavares. |
| BLOWFISH | Designed by Bruce Schneier |
| TWOFISH | Designed by Bruce Schneier and derived from Blowfish |
| CAMELLIA128, CAMELLIA192, and CAMELLIA256 | Designed by Mitsubishi Electric and NTT in Japan. Its name is derived from the flower camellia japonica. |
Block ciphers and stream ciphers are the two main types of symmetric encryption algorithms. Block ciphers operate on blocks of fixed-size plaintext data, and divide the data into fixed-size blocks before encrypting it. Stream ciphers, on the other hand, operate on plaintext data one bit or byte at a time, and encrypt it as it is being transmitted.
Symmetric encryption solves many security problems, including confidentiality, which ensures that only the intended recipient can read the encrypted message. Other security problems that symmetric encryption can help solve include integrity, which ensures that the data has not been tampered with, and authentication, which verifies the identity of the sender and receiver of the message.
Confidentiality: refers to the protection of sensitive information from unauthorized access. It ensures that only authorized parties can access and view the data, keeping it secure from disclosure to third parties.
Integrity: refers to the protection of data from unauthorized modification, deletion, or tampering. It ensures that the data remains accurate, complete, and consistent over its entire lifecycle.
Authenticity: refers to the assurance that data, information, or communication is genuine and has not been altered or falsified. It ensures that the data is coming from the expected source and has not been tampered with during transmission.
GNU Privacy Guard (GnuPG or GPG) and OpenSSL are software tools used to encrypt and decrypt files.
GnuPG (GPG) & OpenSSL encryption:
gpg --symmetric --cipher-algo AES256 message.txt
openssl aes-256-cbc -e -in message.txt -out encrypted_message
- (encrypts the file message.txt using the AES256 cipher and saves the encrypted file as message.txt.gpg.)
GnuPG (GPG) & OpenSSL decryption:
gpg --output original_message.txt --decrypt message.txt.gpg
openssl aes-256-cbc -d -in encrypted_message -out original_message.txt
- (decrypts the file message.txt.gpg and saves the original message as original_message.txt.)
Both GnuPG and OpenSSL provide options to make encryption more secure, such as using the Password-Based Key Derivation Function 2 (PBKDF2) and specifying the number of iterations to derive the encryption key. These options increase the security and resilience of the encryption against brute-force attacks.
Asymmetric Encryption
Symmetric encryption requires a secure channel for exchanging keys, ensuring confidentiality and integrity. On the other hand, asymmetric encryption allows encrypted message exchange through a reliable channel, with integrity being the main concern.
To use asymmetric encryption, we generate a key pair consisting of a public and private key. The public key is shared with anyone we want to communicate with securely, while the private key must be kept safe and secure.
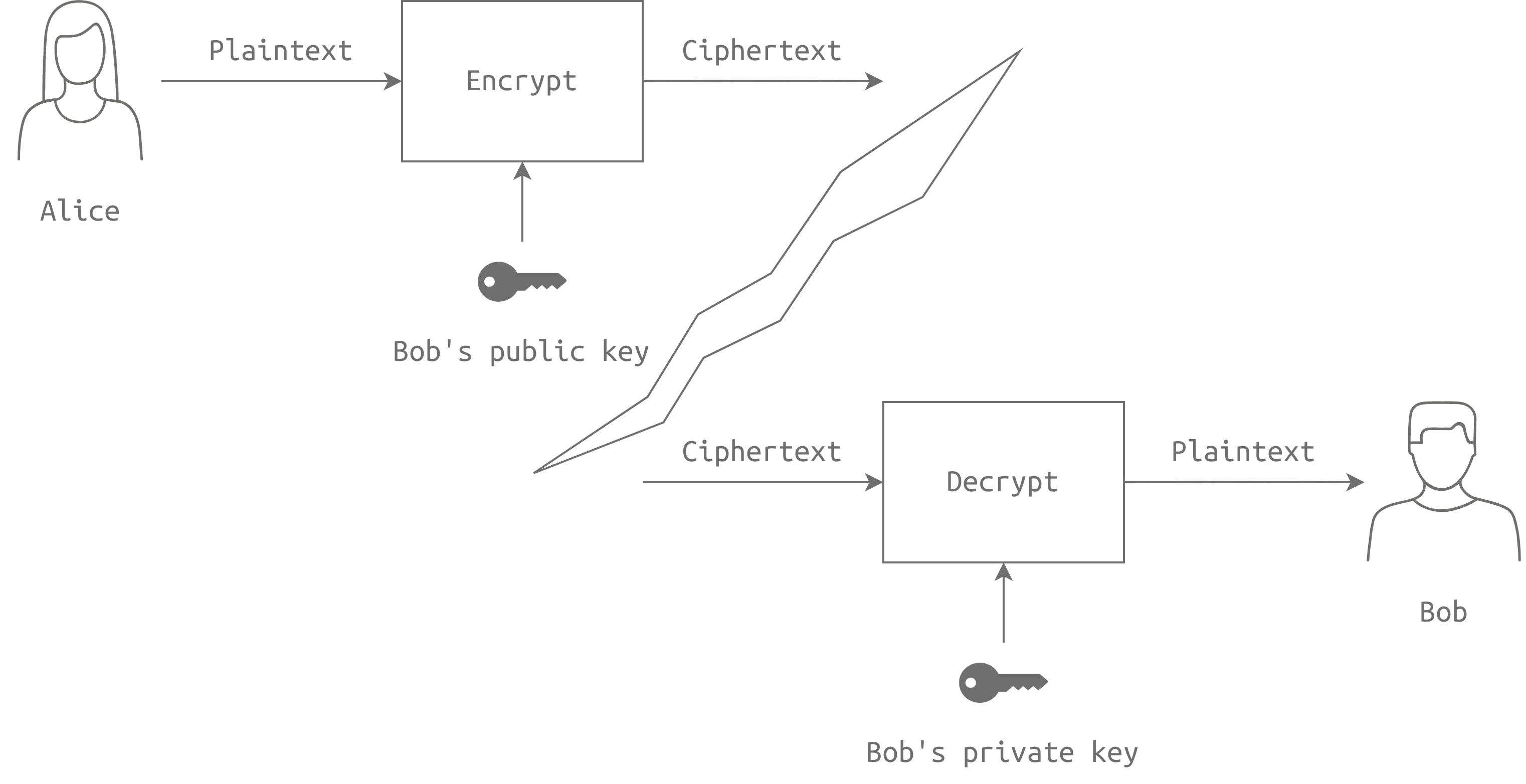
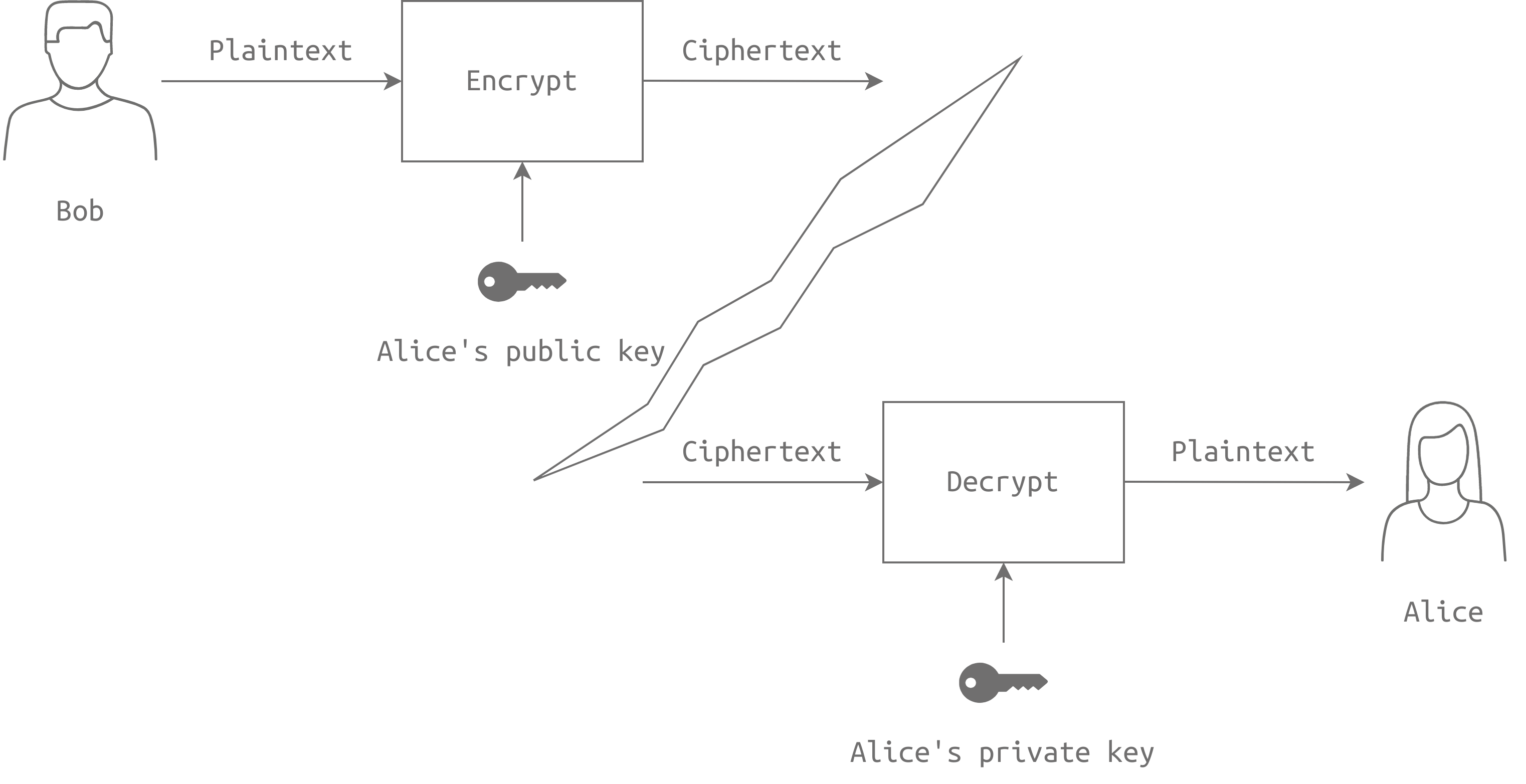
Using the key pair, we can achieve confidentiality by encrypting messages with the recipient's public key and decrypting them with their private key. Asymmetric encryption can also provide integrity, authenticity, and nonrepudiation, ensuring that messages are not altered, can be traced back to the sender, and cannot be denied.
Although asymmetric encryption can be slow for large data, we can use it together with symmetric encryption to achieve security objectives more quickly.
RSA encryption is named after its inventors Rivest, Shamir, and Adleman. It is a popular asymmetric encryption algorithm that relies on the difficulty of factoring large numbers to secure communications. Here's how it works:
- Choose two large random prime numbers, p and q, and calculate N=p*q.
- Select two integers e and d such that e*d=1 mod ϕ(N), where ϕ(N) is the Euler's totient function of N. This generates the public key (N,e) and the private key (N,d).
- To encrypt a value x, the sender calculates y=x^e mod N (modulus).
- The recipient can decrypt y by calculating x=y^d mod N. This step works because of the restrictions on e and d chosen in step 2.
RSA encryption relies on the secure generation of large random prime numbers and is readily available through software libraries. RSA security depends on the difficulty of factoring large numbers, so the key sizes should be significant, for example, 1024 bits or more.
As an example, if Bob chooses p=157 and q=199, then N=31243, and e=163 and d=379. The public key is (31243,163), and the private key is (31243,379). If the value to encrypt is x=13, Alice calculates y=13163 mod 31243=16342 and sends it to Bob. Bob decrypts it by calculating x=16341379 mod 31243=13.
Generate an RSA private key with a key size of 2048 bits and save it as "private-key.pem":
openssl genrsa -out private-key.pem 2048
Extract the public key from the private key and save it as "public-key.pem":
openssl rsa -in private-key.pem -pubout -out public-key.pem
View the RSA variables of the private key:
openssl rsa -in private-key.pem -text -noout
Encrypt a plaintext file "plaintext.txt" using the recipient's public key "public-key.pem" and save the ciphertext as "ciphertext":
openssl pkeyutl -encrypt -in plaintext.txt -out ciphertext -inkey public-key.pem -pubin
Decrypt the ciphertext "ciphertext" using the recipient's private key "private-key.pem" and save the plaintext as "decrypted.txt":
openssl pkeyutl -decrypt -in ciphertext -inkey private-key.pem -out decrypted.txt
Diffie-Hellman Key Exchange
Alice and Bob need to agree on a secret key, but they're communicating over an insecure channel where eavesdroppers can read their messages. So, how can they agree on a secret key? One way is to use the Diffie-Hellman key exchange.
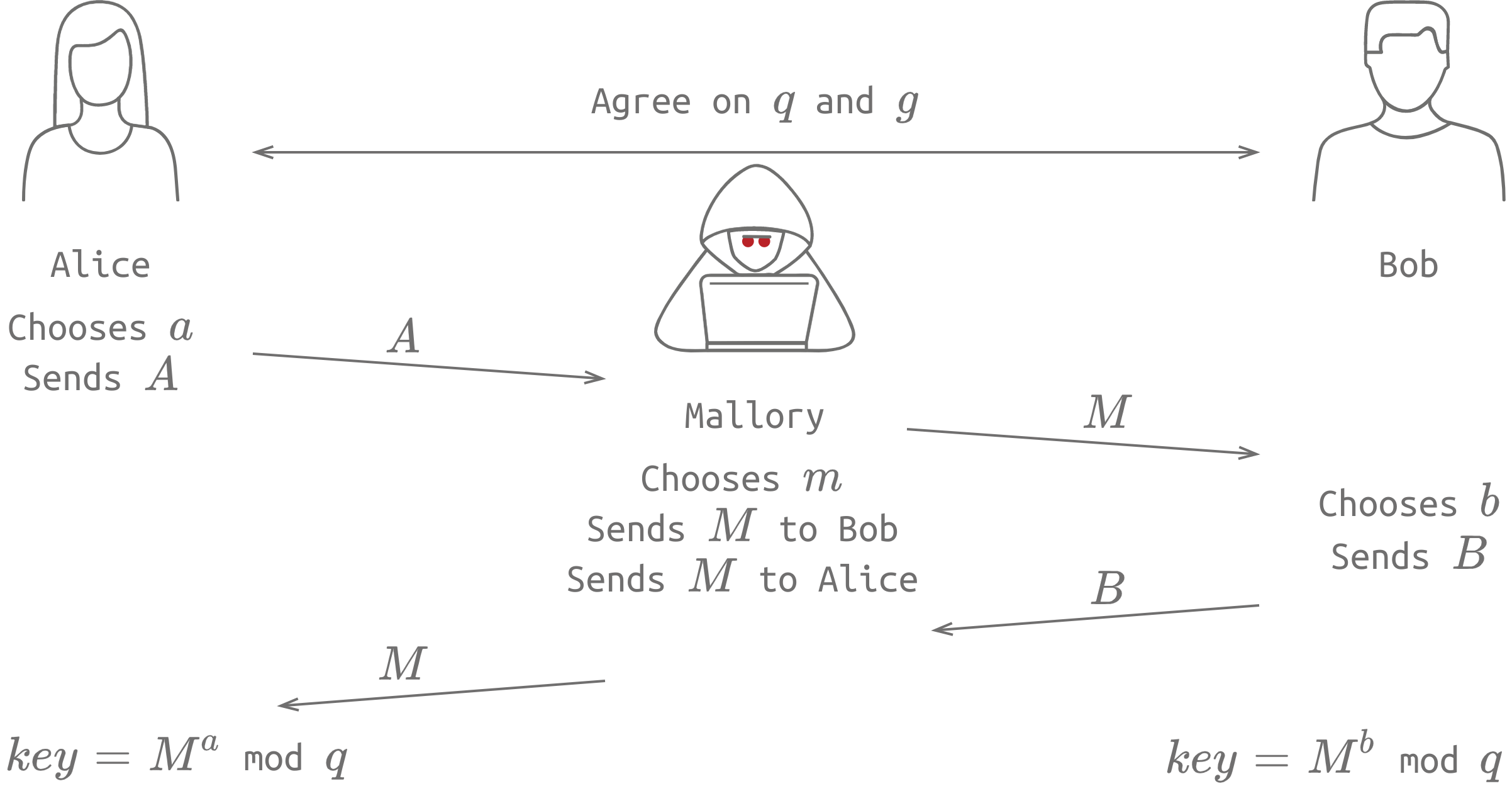
Diffie-Hellman is an asymmetric encryption algorithm that allows for the exchange of a secret over a public channel. Here's how it works: Alice and Bob agree on a prime number (q) and a generator (g). Then, Alice chooses a random number (a) and calculates A = (g^a) mod q. She sends A to Bob, but keeps a a secret. Bob does the same thing, choosing a random number (b) and calculating B = (g^b) mod q. He sends B to Alice, but keeps b a secret.
Then, Alice and Bob each calculate the secret key using the other person's number and their own secret number. So, Alice calculates key = (B^a) mod q, while Bob calculates key = (A^b) mod q. They end up with the same key, which they can use to encrypt their messages.

Even though an eavesdropper can see q, g, A, and B, they won't be able to calculate the secret key without knowing a or b. And, if q is a large enough prime number, it's infeasible to find a or b even if you know the other values.
openssl dhparam -in dhparams.pem -text -noout
Diffie-Hellman is a great way to agree on a secret key over an insecure channel, but it's vulnerable to a Man-in-the-Middle (MitM) attack, where an attacker intercepts the communication and pretends to be Alice to Bob and vice versa. So, it's important to use additional security measures to prevent MitM attacks.
Hashing Function
A cryptographic hash function is an algorithm that takes any amount of data and turns it into a fixed-size output, called a message digest or checksum. For example, the SHA256 algorithm generates a 256-bit (32-byte) checksum, usually expressed in 64 hexadecimal digits.
Hash functions have many uses, such as storing passwords securely and detecting file modifications or transfer errors. By storing a password hash instead of the plain text password, we can protect against data breaches. Even small modifications to a file will result in a completely different hash value, making it easy to detect any tampering.
Some of the secure hashing algorithms in use today include SHA224, SHA256, SHA384, SHA512, and RIPEMD160. However, older algorithms like MD5 and SHA-1 are considered broken since they can be exploited to create hash collisions. This means that an attacker could create a new message with the same checksum as the original, making it impossible to detect tampering.
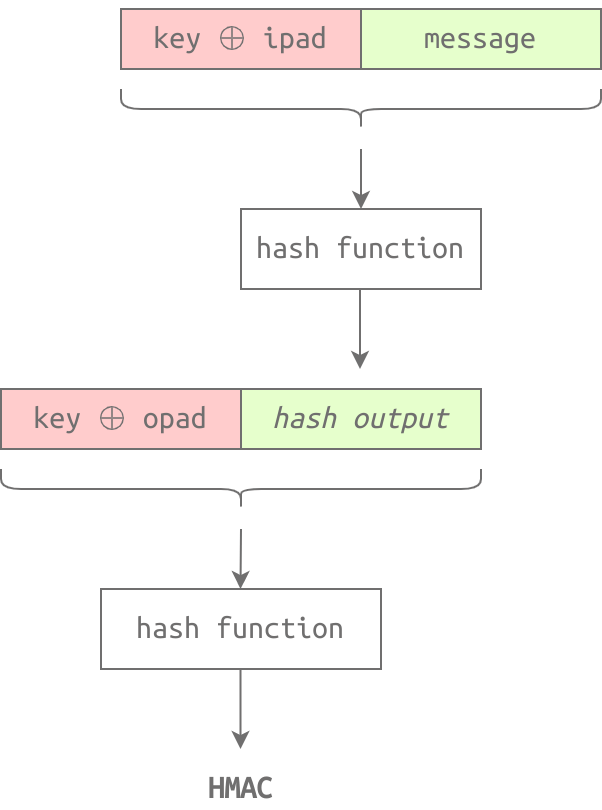
HMAC is a way to authenticate messages using a hash function and a secret key. To calculate an HMAC, you need a secret key, an inner pad, and an outer pad. These pads are constant strings used in the calculation process. To calculate an HMAC, you follow several steps, including XORing the key and pads and applying the hash function.
To make this process easier, there are tools available on Linux systems like hmac256 and sha256hmac. You can use these tools to calculate an HMAC using different keys. By using HMAC, you can verify the authenticity of a message without compromising the security of the secret key.
hmac256 [pass] message.txt
PKI and SSL/TLS
By using a key exchange like Diffie-Hellman, we can securely agree on a secret key for confidential communication. However, this method is vulnerable to a Man-in-the-Middle attack, which highlights the need for a way to confirm the other party's identity. This is where Public Key Infrastructure (PKI) comes in.
When browsing a website over HTTPS, the lock icon in the browser indicates that the connection is secured with a valid certificate. This certificate is signed by a Certificate Authority (CA), such as DigiCert Inc., to confirm its validity.
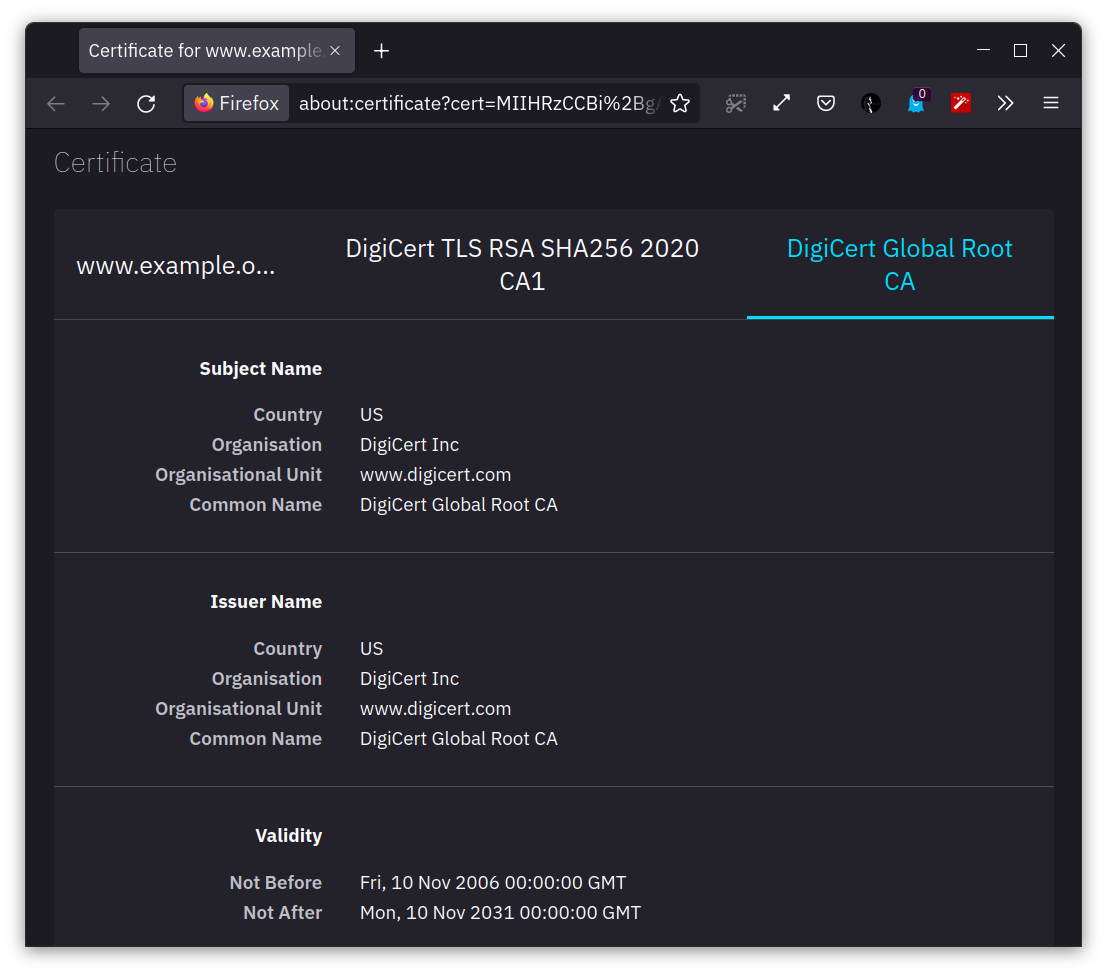
To get a certificate signed by a CA, a Certificate Signing Request (CSR) is generated, and the public key is sent to the CA for signing. It's important that the recipient recognizes and trusts the CA that signed the certificate to ensure secure communication. Thankfully, our browser already trusts reputable CAs like DigiCert Inc., which allows for secure browsing without security warnings.
To generate a certificate signing request using OpenSSL:
openssl req -new -nodes -newkey rsa:4096 -keyout key.pem -out cert.csr
req -newcreate a new certificate signing request-nodessave private key without a passphrase-newkeygenerate a new private keyrsa:4096generate an RSA key of size 4096 bits-keyoutspecify where to save the key-outsave the certificate signing request
To generate a self-signed certificate for testing purposes:
openssl req -x509 -newkey -nodes rsa:4096 -keyout key.pem -out cert.pem -sha256 -days 365
To view the details of a certificate file:
openssl x509 -in cert.pem -text
Authenticating with Passwords
Let's explore how cryptography can enhance password security. By utilizing PKI and SSL/TLS, we can ensure that our login credentials remain secure as they move across the network, safeguarding data in transit. However, we must also consider how to protect passwords when they are saved in a database, that is, data at rest.
Storing passwords directly in a database is the least secure approach, as a data breach could expose users' passwords. Therefore, it's better to store the username and a hashed version of the password in the database. With this approach, if a data breach occurs, only the hashed versions of the passwords are exposed. Since hash functions are irreversible, attackers must repeatedly try different passwords to find the one that yields the same hash value.
Although this approach seems secure, the availability of rainbow tables has made it vulnerable. A rainbow table contains a list of passwords and their corresponding hash values, allowing an attacker to easily recover a password's original value. To prevent this, we can add salt, which is a random value appended to the password before hashing. By using hash(password + salt) or hash(hash(password) + salt), we can make the password storage more secure. Additionally, we can use a key derivation function like PBKDF2 to further strengthen password security.
In summary, by using these methods, we can significantly increase the security of password storage and reduce the likelihood of data breaches.
Salting is adding a unique random string of characters to a password before it's hashed and stored alongside the hashed password in the database.
Peppering involves adding a fixed secret value to a password before it's hashed, but the secret value is kept secret by the application and not stored in the database. Both techniques make it harder for attackers to crack passwords.
Cryptography and Data - Example
Let's explore what happens when we log into a website securely using HTTPS.
To establish a secure connection, the client requests the server's SSL/TLS certificate, which is sent back by the server. The client then verifies the validity of the certificate by checking if it's signed and encrypted by a trusted third party.
If the certificate is valid, an SSL/TLS handshake is initiated, allowing the client and server to agree on a secret key and symmetric encryption algorithm for secure communication.
Finally, the client uses the secure session to send login credentials to the server, which then checks if they match by comparing the hashed version of the password saved with a random salt for added security. This approach ensures that even if there is a breach, the passwords are challenging to retrieve.
Source: TryHackme